Es más que sabida la impericia generalizada que el gremio psicológico padece en el campo de las matemáticas y no se diga el uso de la estadística. Causal de esta distancia no es sólo un tema de pereza profesional sino de una enemistad sembrada durante la segregación de la psicología en “escuelas” en pro de la defensa de las ideas en lugar del avance del conocimiento.
Así, los psicólogos veían en la estadística al Caballo de Troya de los conductistas, los biologisistas y los psiquiatras DSM-cuatristas. Afortunadamente los tiempos han cambiado y el negacionismo estadístico está desapareciendo rápidamente de las universidades. Pero para aquellos que todavía adolecen de este mal de nuestra profesión, aquí 5 razones para que se animen a amigarse nuevamente como los números:
1. El paciente sigue siendo un ser humano
Quizá la negativa más popular para desestimar el uso de la estadística en psicología es por su efecto “deshumanizante”. Ya hemos escuchado en este portal más de una ocasión como los resultados de estudios “dejan de un lado la subjetividad y los casos particulares”. ¡Justo para eso sirve la Prueba Z! A diferencia de otro tipo de pruebas que requieren de medidas de tendencia central (media, moda, mediana) y medidas de dispersión (varianza, cuartil, desviación estándar), la Prueba Z no hace uso de ellas, porque considera cada caso como individual. El paciente “Carlos” es el “Paciente 1” y la paciente “Susana” es la “Paciente 2” y en ningún momento vamos a promediarlos, sumarlos o dividirlos ya que no se puede tener “4.8” pacientes.
El autómata de la película HUGO (Scorsese, 2011) ilustra el temor de la reducción de la subjetividad al mero automatismo y la cosificación del sujeto.
2. Impide que el psicólogo se deje llevar por las apariencias
El juicio personal es muy valioso en la práctica profesional, pero no por ello está exento del sesgo por confirmación: darle más peso a la evidencia que confirma nuestras ideas y demeritar la evidencia que va en contra de ellas. Por ejemplo, una reconocida psicóloga que sale en la TV afirma que hay una epidemia de depresión este mes de febrero, ya que de cada 10 pacientes que recibe, 5 padecen depresión. Sin embargo, otro psicólogo que trabaja en consulta externa de un hospital, asegura que de los últimos 31 pacientes que ha recibido, 6 padecen depresión. ¿Quién de los dos tiene la razón? Hagamos primero un razonamiento empírico:
Empíricamente, diríamos que la Psicóloga 1 tiene un 50% de casos con depresión y el Psicólogo 2 tiene un 19%. La lógica nos diría que esta diferencia se debe a que en un hospital se reciben pacientes mucho más diversos que en la consulta privada, pero ¿es esto cierto? La Prueba Z nos permite comparar proporciones respetando la diferencia de tamaño entre poblaciones, es decir, permite confirmar o refutar el supuesto de que el 50% de 10 pacientes es diferente del 19% de 31 pacientes.
3. No se necesitan tablas de valores críticos ni software estadístico
La Prueba Z es tan noble que no requiere de una tabla de valores críticos, de grados de libertad ni de valores p. El valor crítico siempre es el mismo para comparar proporciones de dos grupos con un error de 0.05. Este valor crítico es 1.96 y su interpretación es tan fácil como saber si un número es “mayor o menor a 1.96”.
Siguiendo el ejemplo de la Psicóloga 1 y el Psicólogo 2, computar los valores n1, n2, x1 y x2 es todo lo que se necesita para calcular Z:
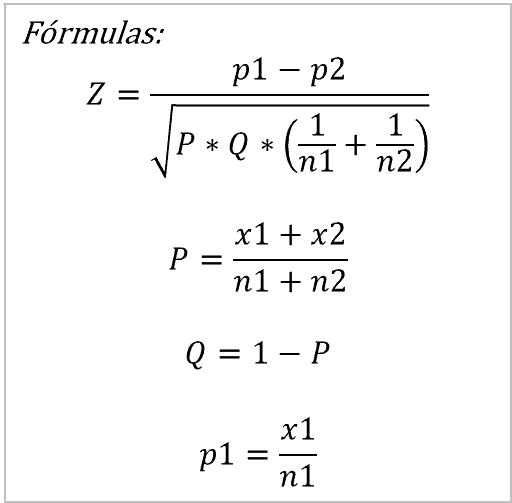
En este caso el resultado es 1.90. Dado que 1.90 es menor que el valor crítico 1.96, entonces podemos asegurar que las proporciones de pacientes deprimidos para ambos grupos (psicólogos) son equivalentes. Es decir, que la psicóloga de la TV está sobre-estimando la proporción de sus pacientes con depresión ya que es equivalente a la proporción de pacientes con depresión en un hospital.
4. Permite tomar decisiones donde la intuición podría ser peligrosa
La facilidad de la Prueba Z ayuda a que los psicólogos aprovechen las herramientas clínicas al máximo, evitando la famosa decisión de Procusto (ajustar el caso a la teoría) que tanto daño ha hecho a la práctica clínica. Por ejemplo, supongamos que tenemos una paciente con ataques de pánico. El primer mes de diagnóstico y contención le damos un diario de paciente para que registre el número de días con ataques de pánico. Al final del mes resulta que de 30 días, sufrió ataques de pánico en 23, por lo que decidimos iniciar tratamiento de psicoeducación. Después del primer mes de tratamiento revisamos el diario de la paciente y vemos que los días con ataques de pánico se redujeron a 15. Pese a ello, la paciente reporta no sentir mejoría. ¿La paciente en verdad mejoró, o esta reducción de 8 días sin ataques de pánico justificaría un cambio de tratamiento? Veamos lo que obtenemos con la prueba Z:
Cálculo de la Prueba Z con una sencilla hoja en MSExcel:
Como se podrá ver, esta reducción de 8 días sin ataques de pánico refuta la hipótesis de que no ha habido mejoría (Ho= el número de ataques de pánico es equivalente antes y durante el tratamiento) y por el contrario permite aceptar la hipótesis de que el tratamiento está surtiendo efecto (Ha= el número de ataques de pánico es mayor antes y menor durante el tratamiento). Este tipo de controles permite enriquecer decisiones clínicas más sólidas e incluso explicarlas con transparencia al paciente.
5. ACP tiene un archivo listo para usarse
La Prueba Z forma parte del temario de prácticamente todas las universidades en la formación de psicólogos, ya sea en las asignaturas de Métodos de Investigación o en el Seminario de Tesis, sin embargo su uso en la actividad cotidiana –aunque necesaria- es poco frecuente. Al entrevistar a nuestros alumnos de por qué la dificultad de trabajar con una herramienta tan amigable, surgió la idea de hacer un sencillo archivo de MSExcel con la fórmula para que los alumnos simplemente integren los cuatro valores clave que requiere la Prueba Z:
Tamaño del grupo 1 (n1)
Tamaño del grupo 2 (n2)
Número de casos de interés del grupo 1 (x1)
Número de casos de interés del grupo 2 (x2)
Con estos cuatro valores el valor Z se calcula automáticamente y se puede rechazar o refutar la hipótesis nula Ho con toda facilidad. Este archivo ya está disponible en nuestro ToolBox libre de descarga para todos nuestros lectores. Esperemos que con esta herramienta los psicólogos se reconcilien mucho más rápido con el uso de la estadística en la práctica cotidiana.
